
The rules for Natural logarithm
Are the rules for natural log the same as logarithms of other bases? Yes, all logarithms follow the same rules regardless of base. Those are:
\begin{equation}
ln(ab)=ln(a)+ln(b)
\end{equation}
\begin{equation}
ln(\frac{a}{b})=ln(a)-ln(b)
\end{equation}
\begin{equation}
ln(b^c)=c ln(b)
\end{equation}
\begin{equation}
ln(a)=\frac{log_b(a)}{log_b(e)}
\end{equation}
The natural logarithm is simply the logarithm of base e. In other words $log_e(a)=ln(a)$ by definition. Recall that e is the irrational number 2.7182.....
You have probably learned already the logarithm of base 10, $log(x)$, which is the inverse function of the exponential
\[y=10^x\]
The natural logarithm $ln(x)$ is simply log base e or the inverse function of $y=e^x$.
Recall that the definition of an inverse function is \[f^{-1}[f(x)]=x\] Or in plain English the inverse function "undoes" its original function. So in the case of the natural logarithm \[ln(e^x)=x\]
What the heck is the number e? Why do we care?
The natural logarithm is not taught well in most math classes. The significance is generally skipped which leaves the student feeling like it’s a totally arbitrary concept. The key to understanding the natural logarithm is understanding the significance of the irrational number e = 2.7182……
e is a number with amazing properties and is of central importance to the field of mathematics. e is generally used in the exponential equation
\[y=e^x\]
which has the following graph:

This graph has a property that no other graph in the universe has: the output y is equal to the slope of the tangent line for every value of x. Let me explain what that means.
I will assume the reader has an understanding of the slope of a line, or its steepness. You’ll notice that the graph above is not a line, it’s a curve. Can a curve have slope? Yes, we refer to the slope at a point, something you’ll learn much more about when you take calculus next year. Here is a graph of a tangent line of $e^x$ at one particular x value:
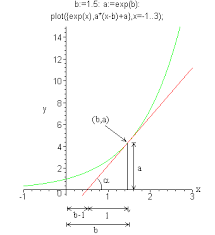
You can see that the slope is different at every point on the curve, increasing with x. You can visualize the red line getting steeper as you move the tangent point to the right. For each x value, there is an associated slope and y value. The insane thing about $y=e^x$ is the slope and y value are the same number for every value of x!
Another way of saying this is the rate of change of the function is the same as its output for all inputs. $y=e^x$ is the only function in existence with this property. This is very useful for calculating things such as compound continuous interest or anything that is in a constant state of change.
Why?
Well, something that is constantly changing (like the value of your bank account accruing compound continuous interest) seems like a very complicated and confusing thing to calculate. However, because the slope of $e^x$ is always equal to its corresponding y value you can get the rate of change by simply plugging in the x value.
For example, the slope of the tangent line of $e^x$ at $x=1$ is e (you'll have to take my word for it until you take calculus, at which point we can easily prove it). What do you get when you plug 1 into $e^x$? You get e, the slope of the tangent line is equal to the corresponding y value. This is true for all values of x, and that is what makes $e^x$ so special. In higher-level math classes, you will find that this property also makes $e^x$ the solution to many types of equations.
I hope this clears up the significance of the natural logarithm. For an in-depth derivation of the natural log rules see the FAQ below.
Frequently Asked Questions
Yes, logarithms of all bases follow the same rules above. Recall that $ln(x)$ is simply a log with base e.
\[ln(ab)=ln(a)+ln(b)\]
\[ln(\frac{a}{b})=ln(a)-ln(b)\]
\[ln(b^c)=c ln(b)\]
\[ln(a)=\frac{log_b(a)}{log_b(e)}\]
The main thing to understand is the log rules are a reflection of the exponent rules as they are inverse functions. First let's call $m=ln(a)$ and $n=ln(b)$. Putting these expressions in exponential form we have
\[a=e^m\] and \[b=e^b\]
we can multiply a and b to get
\[ab=e^me^n\] and applying the rule for multiplying exponents we get
\[ab=e^{m+n}\]
Taking the natural log of both sides
\[ln(ab)=ln(e^{m+n})\]
\[ln(ab)=m+n\]
Finally substituting our definitions of m and n we have
\[ln(ab)=ln(a)+ln(b)\]
And there you have it!
The main thing to understand is the log rules are a reflection of the exponent rules as they are inverse functions. First let's call $m=ln(a)$ and $n=ln(b)$. Putting these expressions in exponential form we have
\[a=e^m\] and \[b=e^b\]
we can divide a and b to get
\[\frac{a}{b}=\frac{e^m}{e^n}\] and applying the rule for multiplying exponents we get
\[\frac{a}{b}=e^{m-n}\]
Taking the natural log of both sides
\[ln(\frac{a}{b})=ln(e^{m-n})\]
\[ln(\frac{a}{b})=m-n\]
Finally substituting our definitions of m and n we have
\[ln(\frac{a}{b})=ln(a)-ln(b)\]
And there you have it!
The main thing to understand is the log rules are a reflection of the exponent rules as they are inverse functions. First let's call $m=ln(a). Putting this expression into exponential form we have
\[a=e^m\]
we can raise a to the power of b to get
\[a^b=(e^m)^b\] and applying the exponent rule for powers we get
\[a^b=e^{mb}\]
Taking the natural log of both sides
\[ln(a^b)=ln(e^{mb})\]
\[ln(a^b)=mb\]
Finally substituting our definition of m
\[ln(a^b)=bln(a)\]
And there you have it!
The main thing to understand is the log rules are a reflection of the exponent rules as they are inverse functions. First let's call $m=ln(a). Putting this expression into exponential form we have
\[a=e^m\]
Now lets take the logarithm of both sides with any base we like, let's call it c
\[log_c(a)=log_c(e^m)\]
Using the power rule we can write
\[log_c(a)=mlog_c(e)\]
Solving for m we have
\[\frac{log_c(a)}{log_c(e)}=m\]
Finally substituting our definition of m
\[ln(a)=\frac{log_c(a)}{log_c(e)}\]
And there you have it!
Nope! There are no logarithms on the SAT whatsoever.
The ACT occasionally has logarithms in the more difficult sections of the exam.
No. There are no natural logarithms on the PSAT.

