
Geometry is an essential branch of mathematics that has applications across many important disciplines such as physics, astronomy, architecture, engineering, and computer science. Geometry is the study of how points, lines, and shapes are distributed throughout space. It is also a subject that many students struggle with as it uses a different part of the brain than algebra. Students who are visual learners tend to excel in geometry, while students that prefer to follow instructions are better in algebra. As math tutors we see students make the same handful of geometry mistakes over and over again. Here are the top 5 geometry mistakes and how to fix them forever.
5 Most Common Geometry Mistakes
1. Not knowing your reference angle when using S.O.H.C.A.H.T.O.A.
S.O.H.C.A.H.T.O.A. is an acronym for three important equations: sinθ = opp/hyp, cosθ = adjacent/hyp, and tanθ = opp/adj. Note that opposite and adjacent refer to an angle in a triangle. This could be any of the three possible angles in a triangle. One of the most common geometry mistakes is not knowing what angle in the triangle is being used as the reference angle. For example:
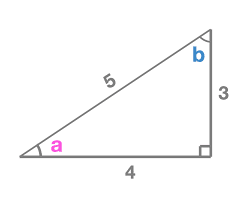
A common geometry mistake would be to write sin(b)= ⅗. In this case, the student used the wrong reference angle. When b is the reference angle, the opposite side of b is 4 and the adjacent side is 3. Therefore the correct statement is sin(b)= ⅘.
In the event that angle a is the reference angle, then the opposite side becomes 3, and the adjacent side becomes 4.
As you can see, when using S.O.H.C.A.H.T.O.A. it is important first to know which angle you are using when constructing your trigonometric relationships. The opposite and adjacent sides depend on which angle you are using.
2. Not knowing your postulates and theorems for proofs.
Proofs are the most universally hated topic in geometry. The reason is that, unlike algebra, there is no one set way to solve a proof. Often there are many ways, and students don’t like this. They feel like there is no procedure to follow and they have to just figure it out by brute force.
Not knowing your theorems and postulates makes it all the more difficult. Therefore it’s best to memorize them all before attempting the proof. Often knowing the theorems and postulates will help guide you through the proof. Here’s a great resource with all the postulates and theorems you need in one place.
3. Confusing triangle congruence with similarity.
Every geometry student learns triangle and congruence and similarity theorems. However, a common mistake we math tutors see is getting congruence and similarity confused.
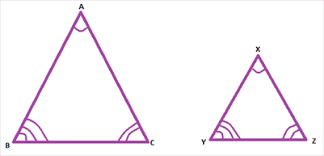
For example, AAA (angle, angle, angle) similarity states that two triangles with three congruent angles are similar. However, they are not necessarily congruent. Many students make the mistake of thinking AAA means congruent triangles.
As you can see in the diagram below, all angles are congruent. However, the triangles themselves clearly are not. Similar triangles have the same shape but can be different sizes.
4. Not using the correct units.
Geometry deals with dimensions: length, area, and volume. Each of these has a different set of units, as they measure different quantities. Length has units of distance, such as meters. Area has units of distance squared, such as m^2. Finally, volume has units of distance cubed, such as m^3.
One of the most common geometry mistakes is to use units of length for an area or volume. For example, a problem might ask for the area of a square:
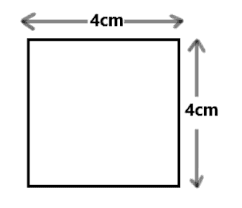
The most common geometry mistake would be for the student to answer A = 16 cm. Centimeters is a unit of length and cannot measure area. The correct answer is A = 16 cm^2.
A square centimeter is a 1cm x 1cm square which can be used to measure area. In the example above it would take 16 of these 1cm x 1cm squares to cover the entire 4cm x 4cm square. That’s how you measure area!
5. Not converting degrees into radians when measuring arc length.
Many students do not understand what a radian is. It’s simply the angle that’s created by an arc with the same length as the radius. See the diagram below:
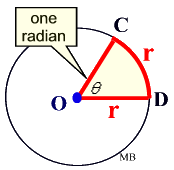
The mistake we math tutors see frequently is in using the formula s = r Θ. The angle theta must be in radians for the equation to hold true. Many geometry problems will give the angle in degrees. That angle must be converted to radians first, otherwise the formula does not work.
These are the most common geometry mistakes that we math tutors see. We end up teaching these 5 topics over and over again. I really hope this article helps you to avoid these mistakes and make big progress in your geometry class. Good luck!


