The quadratic formula is one of, if not, the first “big” formulas introduced in algebra. It looks pretty daunting:
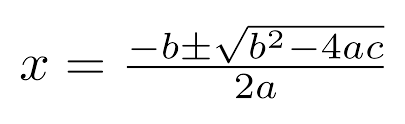
Many students have get a lot of anxiety when they see this. However, it is a powerful analytical tool that helps us find the roots, or zeros, of a quadratic function. These are the points where it crosses the x-axis.
Recall that factoring quadratics into binomials allows us to take a quadratic equation of the form:
$y=ax^2+bx+c$ to the factored form $y=(x+f)(x+g)$
This can usually be done quickly by hand if the quadratic is simple enough. However, not all quadratics can be easily factored. It's in these cases that you should use the quadratic equation.
Most students simply memorize the formula and plug numbers in. It's much more fun to understand where this all-important formula comes from.
Deriving the Quadratic equation
We will demonstrate a simple quadratic formula proof. Starting with the general quadratic form:
begin{equation} y=ax^2+bx+c=0 end{equation}
Since we are looking for where our parabola intersects the x-axis, we set $y=0$. Our first step is to move the constant to the other side of the equation and divide through by the leading coefficient “a” in order to have a nice 1 leading coefficient in front of the $x^2$.
begin{equation} ax^2+bx=-c end{equation}
begin{equation} x^2+frac{bx}{a}=-frac{c}{a} end{equation}
Our next step is the trickiest: completing the square. We purposefully add the term $-frac{b}{2a}$ to both sides which allows the left hand side to be factored
begin{equation} x^2+frac{bx}{a}+frac{b^2}{4a^2}=-frac{c}{a}+frac{b^2}{4a^2} end{equation}
Factoring the left hand side we have
begin{equation} left(x+frac{b}{2a}right)^2 = -frac{c}{a}+frac{b^2}{4a^2} end{equation}
Combining the right side under a single denominator gives
begin{equation}left(x+frac{b}{2a}right)^2 = frac{b^2-4ac}{4a^2} end{equation}
Next, we take the square root of both sides. We must remember that taking a square root produces two roots, one negative and one positive, hence the $pm$.
begin{equation} sqrt{left(x+frac{b}{2a}right)^2} = pmsqrt{frac{b^2-4ac}{4a^2}} end{equation}
On the left side the square root cancels the square on the binomial.
begin{equation}left(x+frac{b}{2a}right) = pmfrac{sqrt{b^2-4ac}}{2a} end{equation}
From here we subtract both sides by $frac{-b}{2a}$ term and consolidate it under the same denominator. And we have arrived:
begin{equation} x =pmfrac{sqrt{b^2-4ac}}{2a}-frac{b}{2a} end{equation}
begin{equation} x=frac{-b pm sqrt{b^2-4ac}}{2a} end{equation}
Pretty neat. Now we can actually dive a little deeper into the equation to gain some further insights about quadratics/parabolas.
Understanding the Quadratic Equation

The Roots
The first thing that stands out with the quadratic formula is its relation to the vertex form. Keen readers will remember the vertex form being
$y= a(x-h)^2 + k$ with the vertex of the parabola being at (h,k)
The variable h is special because it is also the x-value denoting the axis of symmetry of the parabola. When deriving the vertex form we find that $h=-frac{b}{2a}$. Look familiar? Mathematicians like to write equations in the most simplified and condensed form. However, let's take one step back in the derivation to reveal something interesting:
$x =-frac{b}{2a}pmfrac{sqrt{b^2-4ac}}{2a}= h pmfrac{sqrt{b^2-4ac}}{2a}$
There it is! But how does this help? The purpose of the quadratic formula is to give us the roots of the parabola and in this form, we can see that the two roots are equidistant from the axis of symmetry h.
$x_1$ = $h + frac{sqrt{b^2-4ac}}{2a}$ and $x_2$ = $h - frac{sqrt{b^2-4ac}}{2a}$
One root is to the left, and the other root is the same amount to the right. We can better see this graphically, and it stands to reason since a parabola is symmetric and so would its roots be too.
The Discriminant
There is a hidden insight in the second term. Considering all parabolas, they all either have two real distinct roots, one repeated root, or no roots at all if it does not cross the x-axis. Part of the quadratic equation can tell us, the part inside the square root.
$D = b^2 - 4ac$
This is called the discriminant; we will label it as D. Recall the split form of the quadratic formula. Every parabola will have an axis of symmetry, but not all parabolas will have real roots. Combining everything we’ve done so far gives us:
$x = h pmfrac{D}{2a}$
This looks much less scary and more simplified. We can now notice the purpose of the discriminant. This “distance to the roots from the axis of symmetry” is controlled by the discriminant. The larger D gets, the further apart the roots are, and vice versa. This leads to a few questions. What if the discriminant becomes zero, or even negative? Let’s look at those cases.
The first case is that of a positive discriminant, D>0. As we determined above, a positive determinant means our roots exist, are distinct, and are some distance away from h.
$x_1$ = $h + frac{sqrt{D}}{2a}$ and $x_2$ = $h - frac{sqrt{D}}{2a}$
The second case is that of a discriminant of zero, D=0. This will make the second term of the quadratic equation equal to zero, so our roots will now look like:
$x=hpmfrac{0}{2a}$ or $x_1$=$x_2$=$h$
This is known as a repeated root. It is a single point where the vertex just touches the x-axis. We can see this as D became smaller, the two roots converged into one.
Now the last case is the most perplexing, and simple at the same time. That of the discriminant being negative, D<0. Recall that the discriminant belongs inside the square root of the second term, but what is the square root of a negative number? If we plot this quadratic equation on a graph we see that the parabola never touches the x-axis, so when D<0, the parabola has no roots. No real roots at least. The answer to “What is the square root of a negative number?” will be a topic for another time.

Conclusion
The quadratic equation is one of the most important topics you'll learn in your math career. It is essential for all higher-level math classes, so please take the time to understand it as deeply as possible. Good luck!
$x=frac{-bpmsqrt{b^2-4ac}}{2a}$
The quadratic formula is an equation used to solve 2nd order polynomial equations of the form $ax^2+bx+c=0$. It will find the value(s) of $x$ for given constants a, b, and c.
Let's look at an example:
$2x^2-3x-5=0$
In this case $a=2$, $b=-3$, and $c=-5$ (don't forget the minus signs, this is a common mistake).
We now substitute these values into the quadratic equation:
$x=frac{-(-3)pmsqrt{(-3)^2-4(2)(-5)}}{2(2)}$
Simplifying we get
$x=frac{(3)pmsqrt{9+40}}{4}$
$x=frac{3pmsqrt{49}}{4}$
$x=frac{3pm7}{4}$
The $pm$ sign implies that we have two solutions for x. For the first solution you take the plus sign, for the second you take the minus sign to get
$x_1$=$frac{3+7}{4}=frac{5}{2}$
and
$x_2$=$frac{3-7}{4}=-1$
The values $frac{5}{2}$ and -1 solve the equation $2x^2-3x-5=0$.

